SMIs and Doubles
This is a third post in the series of the JIT compiling crash-course. For a context please consider reading the first one and the second.
Goal #
Last time we created very basic bump memory allocator and made our existing code work with floating point double numbers, stored in the allocated heap objects. However floating point numbers are not suitable for some of precision-dependent operations and also, since they are stored in memory, requiring additional memory loads and stores, slowing down the code performance.
Both of this problems could be solved by working with the integers stored in the registers (as we did it in first blog post), which means that we will need to support both types of numbers in our compiler's runtime (doubles and integers).
Tagging #
Let's recall that we are storing both pointers and numbers in the 64bit general
purpose registers (rax, rbx, ...). The main issue here is that, given some
register (say rax), we should be able to tell if it is a pointer to the heap
object (a "boxed value") or an integer itself (an "unboxed value",
Small Integer, or SMI).
Usually, a method called "tagging" is used to solve this. While there are
various ways to implement tagging, including: Nan-Boxing (scroll down
to Mozilla’s New JavaScript Value Representation), Nun-Boxing, and probably
some others, our compiler will just reserve the least significant bit of the
64bit register and put 1 here if the value is a pointer and 0 if it is a
SMI (Small Integer).
Here is an example of this representation:
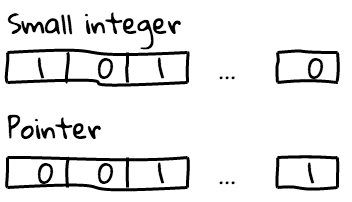
Note that to get the actual value of a SMI ("untag") we will need to shift it
right for one bit (>> 1), and to convert an integer to the SMI - shift left
(<< 1). Using zero for tagging SMIs pays off greatly, since we don't need to
to untag numbers to perform addition and subtraction.
To use tagged pointers to heap objects we'll need to look one byte behind the actual value, which is relatively simple in the assembly language:
// Lets say that tagged pointer is in rbx
// And we're loading its contents into the rax
this.mov('rax', ['rbx', -1]);And just for the convenience - example of untagging SMIs:
// Untag
this.shr('rax', 1);
// Tag
this.shl('rax', 1);And now the most important part that we're going to do a lot - checking if the value is a pointer:
// Test that 'rax' has the last bit
this.test('rax', 1);
// 'z' stands for zero
// Basically, jump to the label if `(rax & 1) == 0`
this.j('z', 'is-smi');
// 'nz' stands for non-zero
// Basically, jump to the label if `(rax & 1) != 0`
this.j('ne', 'is-heap-object-pointer');Reworking previous code #
Using the code from the previous blog post, we can finally proceed to implementing all this recently learned stuff.
First, let's add a convenient helper methods to the assembly context.
function untagSmi(reg) {
this.shr(reg, 1);
};
function checkSmi(value, t, f) {
// If no `true-` and `false-` bodies were specified -
// just test the value.
if (!t && !f)
return this.test(value, 1);
// Enter the scope to be able to use named labels
this.labelScope(function() {
// Test the value
this.test(value, 1);
// Skip SMI case if result is non-zero
this.j('nz', 'non-smi');
// Run SMI case
t.call(this);
// Jump to the shared end
this.j('end');
// Non-SMI case
this.bind('non-smi');
f.call(this);
// Shared end
this.bind('end');
});
};
function heapOffset(reg, offset) {
// NOTE: 8 is the size of pointer on x64 arch.
// We're adding 1 to the offset, because first
// quad word is used to store the heap object's type.
return [reg, 8 * ((offset | 0) + 1) - 1];
};We can hook this methods into the jit.js context by passing them as a helpers
option to the jit.compile() API method:
var helpers = {
untagSmi: untagSmi,
checkSmi: checkSmi,
heapOffset: heapOffset
};
jit.compile(function() {
// We can use helpers here:
this.untagSmi('rax');
this.checkSmi('rbx', function() {
// Work with SMI
}, function() {
// Work with pointer
});
this.mov(this.heapOffset('rbx', 0), 1);
}, { stubs: stubs, helpers: helpers });Allocation #
Now we should make our Alloc stub return tagged pointer. Also we will use the
opportunity and improve it a bit by adding tag and size arguments to the
stub (thus making possible generalized allocation with variable size and tag
in the future):
stubs.define('Alloc', function(size, tag) {
// Save 'rbx' and 'rcx' registers
this.spill(['rbx', 'rcx'], function() {
// Load `offset`
//
// NOTE: We'll use pointer to `offset` variable,
// to be able to update
// it below
this.mov('rax', this.ptr(offset));
this.mov('rax', ['rax']);
// Load end
//
// NOTE: Same applies to end, though, we're
// not updating it right now
this.mov('rbx', this.ptr(end));
this.mov('rbx', ['rbx']);
// Calculate new `offset`
this.mov('rcx', 'rax');
// Add tag size and body size
this.add('rcx', 8);
this.add('rcx', size);
// Check if we won't overflow our fixed size buffer
this.cmp('rcx', 'rbx');
// this.j() performs conditional jump to the specified label.
// 'g' stands for 'greater'
// 'overflow' is a label name, bound below
this.j('g', 'overflow');
// Ok, we're good to go, update offset
this.mov('rbx', this.ptr(offset));
this.mov(['rbx'], 'rcx');
// First 64bit pointer is reserved for 'tag',
// second one is a `double` value
this.mov('rcx', tag);
this.mov(['rax'], 'rcx');
// !!!!!!!!!!!!!!!
// ! Tag pointer !
// !!!!!!!!!!!!!!!
this.or('rax', 1);
// Return 'rax'
this.Return();
// Overflowed :(
this.bind('overflow')
// Invoke javascript function!
// NOTE: This is really funky stuff, but I'm not
// going to dive deep into it right now
this.runtime(function() {
console.log('GC is needed, but not implemented');
});
// Crash
this.int3();
this.Return();
});
});Math stubs #
Also, as we're going to do a bit more book-keeping in math operations to support both SMIs and doubles, let's split it apart and put the code, handling doubles into the stub:
var operators = ['+', '-', '*', '/'];
var map = { '+': 'addsd', '-': 'subsd', '*': 'mulsd',
'/': 'divsd' };
// Define `Binary+`, `Binary-`, `Binary*`, and `Binary/` stubs
operators.forEach(function(operator) {
stubs.define('Binary' + operator, function(left, right) {
// Save 'rbx' and 'rcx'
this.spill(['rbx', 'rcx'], function() {
// Load arguments to rax and rbx
this.mov('rax', left);
this.mov('rbx', right);
// Convert both numbers to doubles
[['rax', 'xmm1'], ['rbx', 'xmm2']].forEach(function(regs) {
var nonSmi = this.label();
var done = this.label();
this.checkSmi(regs[0]);
this.j('nz', nonSmi);
// Convert integer to double
this.untagSmi(regs[0]);
this.cvtsi2sd(regs[1], regs[0]);
this.j(done);
this.bind(nonSmi);
this.movq(regs[1], this.heapOffset(regs[0], 0));
this.bind(done);
}, this);
var instr = map[operator];
// Execute binary operation
if (instr) {
this[instr]('xmm1', 'xmm2');
} else {
throw new Error('Unsupported binary operator: ' +
operator);
}
// Allocate new number, and put value in it
// NOTE: Last two arguments are arguments to
// the stub (`size` and `tag`)
this.stub('rax', 'Alloc', 8, 1);
this.movq(this.heapOffset('rax', 0), 'xmm1');
});
this.Return();
});
});Note that this stub also converts all incoming numbers to doubles.
Compiler #
And back to the compiler's code:
function visitProgram(ast) {
assert.equal(ast.body.length,
1,
'Only one statement programs are supported');
assert.equal(ast.body[0].type, 'ExpressionStatement');
// We've a pointer in 'rax', convert it to integer
visit.call(this, ast.body[0].expression);
// Get floating point number out of heap number
this.checkSmi('rax', function() {
// Untag smi
this.untagSmi('rax');
}, function() {
this.movq('xmm1', this.heapOffset('rax', 0));
// Round it towards zero
this.roundsd('zero', 'xmm1', 'xmm1');
// Convert double to integer
this.cvtsd2si('rax', 'xmm1');
});
}
function visitLiteral(ast) {
assert.equal(typeof ast.value, 'number');
if ((ast.value | 0) === ast.value) {
// Small Integer (SMI), Tagged value
// (i.e. val * 2) with last bit set to
// zero
this.mov('rax', utils.tagSmi(ast.value));
} else {
// Allocate new heap number
this.stub('rax', 'Alloc', 8, 1);
// Save 'rbx' register
this.spill('rbx', function() {
this.loadDouble('rbx', ast.value);
// NOTE: Pointers have last bit set to 1
// That's why we need to use 'heapOffset'
// routine to access it's memory
this.mov(this.heapOffset('rax', 0), 'rbx');
});
}
}
function visitBinary(ast) {
// Preserve 'rbx' after leaving the AST node
this.spill('rbx', function() {
// Visit left side of expresion
visit.call(this, ast.right);
// Move it to 'rbx'
this.mov('rbx', 'rax');
// Visit right side of expression (the result is in 'rax')
visit.call(this, ast.left);
//
// So, to conclude, we've left side in 'rax' and right in 'rbx'
//
if (ast.operator === '/') {
// Call stub for division
this.stub('rax', 'Binary' + ast.operator, 'rax', 'rbx');
} else {
this.labelScope(function() {
// Check if both numbers are SMIs
this.checkSmi('rax');
this.j('nz', 'call stub');
this.checkSmi('rbx');
this.j('nz', 'call stub');
// Save rax in case of overflow
this.mov('rcx', 'rax');
// NOTE: both 'rax' and 'rbx' are tagged at this
// point.
// Tags don't need to be removed if we're doing
// addition or subtraction. However, in case of
// multiplication result would be 2x bigger if
// we won't untag one of the arguments.
if (ast.operator === '+') {
this.add('rax', 'rbx');
} else if (ast.operator === '-') {
this.sub('rax', 'rbx');
} else if (ast.operator === '*') {
this.untagSmi('rax');
this.mul('rbx');
}
// On overflow restore 'rax' from 'rcx' and invoke stub
this.j('o', 'restore');
// Otherwise return 'rax'
this.j('done');
this.bind('restore');
this.mov('rax', 'rcx');
this.bind('call stub');
// Invoke stub and return heap number in 'rax'
this.stub('rax', 'Binary' + ast.operator, 'rax', 'rbx');
this.bind('done');
});
}
});
}
function visitUnary(ast) {
if (ast.operator === '-') {
// Negate argument by emulating binary expression
visit.call(this, {
type: 'BinaryExpression',
operator: '*',
left: ast.argument,
right: { type: 'Literal', value: -1 }
})
} else {
throw new Error('Unsupported unary operator: ' + ast.operator);
}
}To conclude, we are now working with SMIs by default, inlining all operations for the speed's sake, and falling back to the doubles in case of overflow or any other trouble, like trying to sum a double and a SMI!
That's all for now, see you here next time! Here is the full compiler code from this article: github. Please try cloning, running and playing with it! Hope you enjoyed this post.
- Previous: Allocating numbers
- Next: Running node.js + DTrace on FreeBSD